The program code for all parts can be downloaded from github. Note that the full code is not found below - to run this, use github code.
Setting up
I am going to use numpy for matrices and pygame for setting up the screen and drawing onto it, so the first thing to do is
import pygame import numpy as np
To set up a simple object, I have defined a cube in XYZ coordinates that has the size (width, height, depth) of 200. It will be centered at (0,0,0). The nodes (the eight corners of the cube, in 3D space) are thus defined as follows:
node_array = np.array([ [ 100.0, 100.0, 100.0], [ 100.0, 100.0,-100.0], [ 100.0,-100.0,-100.0], [ 100.0,-100.0, 100.0], [-100.0, 100.0, 100.0], [-100.0, 100.0,-100.0], [-100.0,-100.0,-100.0], [-100.0,-100.0, 100.0] ])
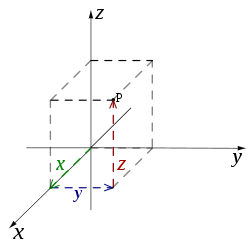
To be clear, I have defined the axis so that X is the horizontal axis, Y is the vertical axis, and Z is the distance frow viewer axis. The standard Cartesian coordinates are usually presented differently:
Cartesian coordinate system. Source: Wikipedia.
Basically, I have rotated the coordinate system above so that X=y, Y=z, and Z=-x. There are other coordinates systems, like polar coordinates, but I will stick to this one.
I want to rotate objects around any of the three axes. To do that, I will define three angles, X, Y, and Z (no surprises here). It is worth noting that, in this system, the order of rotation matters; I am using the order as above. Now it is time to define a VectorObject class.
class VectorObject: """ Position is the object's coordinates. Nodes are the predefined, static definition of object "corner points", around object position anchor point (0,0,0). RotatedNodes are the Nodes rotated by the given Angles and moved to Position. TransNodes are the RotatedNodes transformed from 3D to 2D (X.Y) screen coordinates. @author: kalle """ def __init__(self): self.position = np.array([0.0, 0.0, 0.0, 1.0]) # position self.angles = np.array([0.0, 0.0, 0.0]) self.angleScale = (2.0 * np.pi) / 360.0 # to scale degrees. self.rotationMatrix = np.zeros((3,3)) self.rotateSpeed = np.array([0.0, 0.0, 0.0]) self.nodes = np.zeros((0, 4)) # nodes will have unrotated X,Y,Z coordinates plus a column of ones for position handling self.rotatedNodes = np.zeros((0, 3)) # rotatedNodes will have X,Y,Z coordinates after rotation ("final 3D coordinates") self.transNodes = np.zeros((0, 2)) # transNodes will have X,Y coordinates def setPosition(self, position): # move object by giving it a rotated position. self.position = position def setRotateSpeed(self, angles): # set object rotation speed. self.rotateSpeed = angles def addNodes(self, node_array): # add nodes (all at once); add a column of ones for using position in transform self.nodes = np.hstack((node_array, np.ones((len(node_array), 1)))) self.rotatedNodes = node_array # initialize rotatedNodes with nodes (no added ones required) def increaseAngles(self): self.angles += self.rotateSpeed for i in range(3): if self.angles[i] >= 360: self.angles[i] -= 360 if self.angles[i] < 0: self.angles[i] += 360
Note that there are three sets of object nodes in the class:
- nodes: The original nodes for the object. The fourth element (in addition to X, Y, Z coordinates) will be set to 1.0 to add the position when rotating.
- rotatedNodes: nodes as rotated to the current angles. 3D i.e. X, Y, Z.
- transNodes: rotatedNodes transformed (or flattened) from 3D to 2D screen coordinates. 2D i.e. X, Y only.
Setting up a rotation matrix involves taking a sine and cosine of all the angles. Then the successive rotations are combined in the matrix (see Wikipedia for Euler angles). Having the matrix, it is simple to convert the static nodes to their rotated form: simply perform a dot product of the nodes and the matrix (in rotate).
The matrix and rotation are defined as follows:
def setRotationMatrix(self): """ Set matrix for rotation using angles. """ (sx, sy, sz) = np.sin((self.angles) * self.angleScale) (cx, cy, cz) = np.cos((self.angles) * self.angleScale) # build a matrix for X, Y, Z rotation (in that order, see Wikipedia: Euler angles) including position shift. # add a column of zeros for later position use self.rotationMatrix = np.array([[cy * cz , -cy * sz , sy ], [cx * sz + cz * sx * sy, cx * cz - sx * sy * sz, -cy * sx], [sx * sz - cx * cz * sy, cz * sx + cx * sy * sz, cx * cy ]]) def rotate(self): """ Apply a rotation defined by a given rotation matrix. """ matrix = np.vstack((self.rotationMatrix, self.position[0:3])) # add position to rotation matrix to move object at the same time self.rotatedNodes = np.dot(self.nodes, matrix) def transform(self, midScreen): """ Add screen center. """ # add midScreen to center on screen to get to transNodes. self.transNodes = self.rotatedNodes[:, 0:2] + midScreen
To transform these rotated 3D nodes to a screen-friendly 2D plane, I (in this first phase) contend to just forgetting about the distance axis Z and simply taking the X and Y coordinates and centering the object on screen. In a way this is similar to looking at the object from very far away with a telescope, when the differences in distance from the viewer between the nodes are so small they are meaningless.
Making Something Happen
Now we need to do something with the class defined above. First, I define a couple of keys so that we can easily exit and pause the program:
key_to_function = { pygame.K_ESCAPE: (lambda x: x.terminate()), # ESC key to quit pygame.K_SPACE: (lambda x: x.pause()) # SPACE to pause }
Then let's set up the main class.
class VectorViewer: """ Displays 3D vector objects on a Pygame screen. @author: kalle """ def __init__(self, width, height): self.width = width self.height = height self.screen = pygame.display.set_mode((width,height)) self.fullScreen = False pygame.display.set_caption('VectorViewer') self.backgroundColor = (0,0,0) self.VectorObjs = [] self.midScreen = np.array([width / 2, height / 2], dtype=float) self.target_fps = 60 # affects movement speeds self.running = True self.paused = False self.clock = pygame.time.Clock() def addVectorObj(self, VectorObj): self.VectorObjs.append(VectorObj)
This class basically does two things: It rotates and displays the objects. The main loop run just checks if any of the defined keys were pressed, and runs first rotate and then display:
def run(self): """ Main loop. """ while self.running: for event in pygame.event.get(): if event.type == pygame.QUIT: self.running = False elif event.type == pygame.KEYDOWN: if event.key in key_to_function: key_to_function[event.key](self) if self.paused == True: pygame.time.wait(100) else: # main components executed here self.rotate() self.display() # release any locks on screen while self.screen.get_locked(): self.screen.unlock() # switch between currently showed and the next screen (prepared in "buffer") pygame.display.flip() self.clock.tick(self.target_fps) # this keeps code running at max target_fps # exit; close display, stop music pygame.display.quit()
Rotation actually happens in the VectorObject class as described earlier. The display method then does the following:
- clears the screen by filling it with the background colour.
- for each node, draws a small circle, in white (RGB 255,255,255).
- draws a line between specified nodes to show the cube's edges.
def rotate(self): """ Rotate all objects. First calculate rotation matrix. Then apply the relevant rotation matrix with object position to each VectorObject. """ # rotate and flatten (transform) objects for VectorObj in self.VectorObjs: VectorObj.increaseAngles() VectorObj.setRotationMatrix() VectorObj.rotate() VectorObj.transform(self.midScreen) def display(self): """ Draw the VectorObjs on the screen. """ # lock screen for pixel operations self.screen.lock() # clear screen. self.screen.fill(self.backgroundColor) # draw the actual objects for VectorObj in self.VectorObjs: for node in VectorObj.transNodes: # for each node, draw a small circle (radius = 5) in white (255,255,255) node_int = (int(node[0]), int(node[1])) pygame.draw.circle(self.screen, (255,255,255), node_int, 5) # just for testing purposes - assuming a cube with specific node order, draw edges if np.shape(VectorObj.transNodes)[0] == 8: pygame.draw.aalines(self.screen, (255,255,255), 1, VectorObj.transNodes[0:4,:]) pygame.draw.aalines(self.screen, (255,255,255), 1, VectorObj.transNodes[4:8,:]) for i in range(4): pygame.draw.aaline(self.screen, (255,255,255), VectorObj.transNodes[i,:], VectorObj.transNodes[i+4,:]) # unlock screen self.screen.unlock() def terminate(self): self.running = False def pause(self): if self.paused == True: self.paused = False else: self.paused = True
Note that for all drawing operations, transNodes are used, as they are the 2D screen coordinates. Also note that step 3, drawing the edges, is here just for testing purposes - our cube object only defines the nodes and if they would be in a different order, the edges as defined here might look very strange! This will be fixed in the following part.
Finally, this is the code to set up the cube object and initialize the VectorViewer and then run it.
if __name__ == '__main__': """ Prepare screen, objects etc. """ # set screen size # first check available full screen modes pygame.display.init() # disp_modes = pygame.display.list_modes(0, pygame.FULLSCREEN | pygame.DOUBLEBUF | pygame.HWSURFACE) # disp_size = disp_modes[4] # selecting display size from available list. Assuming the 5th element is nice... disp_size = (1280, 800) vv = VectorViewer(disp_size[0], disp_size[1]) # set up a simple cube vobj = VectorObject() node_array = np.array([ [ 100.0, 100.0, 100.0], [ 100.0, 100.0,-100.0], [ 100.0,-100.0,-100.0], [ 100.0,-100.0, 100.0], [-100.0, 100.0, 100.0], [-100.0, 100.0,-100.0], [-100.0,-100.0,-100.0], [-100.0,-100.0, 100.0] ]) vobj.addNodes(node_array) speed_angles = np.array([1.0, -.3, 0.55]) vobj.setRotateSpeed(speed_angles) position = np.array([0.0, 0.0, 1500.0, 1.0]) vobj.setPosition(position) # add the object vv.addVectorObj(vobj) # run the main program vv.run()
This is what you should see:
When Points Do Not Float
How to do this in the Amiga? Using Assembly, we have access directly to the CPU's instruction set. The eight internal data registers are 32-bit, i.e. they can handle numbers up to 2^32-1 (4,294,967,295), but there is no such concept as decimals. Every number is and has to be an integer. There is no FPU (Floating Point Unit) either. In Python, if we need a sine or cosine of any number, we just call numpy.sin or math.sin, and there we have it. numpy.sin(numpy.pi / 4) = 0.7071067811865476. How is it calculated? I don't know.
In the MC68000 instruction set, there are instructions for adding, subtracting, multiplying, and dividing two integers together (bear in mind that e.g. the Commodore 64 CPU did not have a multiply nor divide instruction, so even this was great). There's certainly no instruction to get a sine. And the sine of any number is, by definition, between -1 and +1. If you only have integers, having a precision of -1, 0, or +1 for your sine and cosine certainly is is not enough for a smooth rotation.
Solving Sine in the Amiga
First of all, a decimal number is nothing more than a big integer divided by another (e.g. 0.2 = 20,000 / 100,000), so scaling is the solution for the missing decimal point. A convenient scaling factor in the MC68000 is $10000 (hexadecimal for 65536 or 2^16), which can be de-scaled by a very quick instruction called swap. Swap simply swaps the two 16-bit parts of a 32-bit register, in effect dividing the 32-bit result with $10000 (when using only the lower 16 bits and discarding the higher 16 bits).
To get a sine for x, there are a number of methods. I used a Taylor series as follows (see link):
And as accuracy is not that critical a factor here, the series can basically be terminated at the fourth, or even third, term. However, care must be taken as the 32-bit data register soon overflows if you raise almost anything to the 7th power. Anyway, this would be way too slow for real-time calculation - multiplications are quite slow. A pre-calculated table is needed. Let's say we divide the full circle to 360 degrees and calculate a sine for all of them, and store the results in memory. Then, when a sine for angle 124 degrees is needed, we just pick the number which is 124 * 2 bytes (as the numbers take 2 bytes each) away from the start of our sine table! Easy and, even more importantly, very fast!
Of course, we need the cosine as well. Luckily - well, actually, it has nothing to do with luck, but still: cos(x) equals sin(x + 90 degrees), so we can use the same table just adjusting the offset.
Usually, it was more convenient to precalculate the sine table and add it to the program code as data than to actually include the precalculation routine to the code.
Next: Part II: Surfaces and Perspective.
Acknowledgement: I took inspiration from Peter Collingridge's blog.
Of course, we need the cosine as well. Luckily - well, actually, it has nothing to do with luck, but still: cos(x) equals sin(x + 90 degrees), so we can use the same table just adjusting the offset.
Usually, it was more convenient to precalculate the sine table and add it to the program code as data than to actually include the precalculation routine to the code.
Next: Part II: Surfaces and Perspective.
Acknowledgement: I took inspiration from Peter Collingridge's blog.

No comments:
Post a Comment